Click here for 12
more years of problems
LSC MS POTW
2019-20 School Year
The school year has come to an end. Look for the POTW again next
year for Volume 14.
Scroll down for earlier problems
Problem 34
A 2-mile long train travels at 40 miles per hour through a
1.5-mile long tunnel. How long will it take the train to completely pass
through the tunnel?
Click here for video
solution!
Problem 33
This
problem is from the Latin Middle School Math Contest: "Math is the Scene
in 2015"
Alice can eat 15% of a pizza in 15
minutes. Steven can eat 20% of a pizza in 25 minutes. How many minutes will it
take Alice and Steven to eat a whole pizza together? Write your answer as a
mixed number.
Click here for video solution!
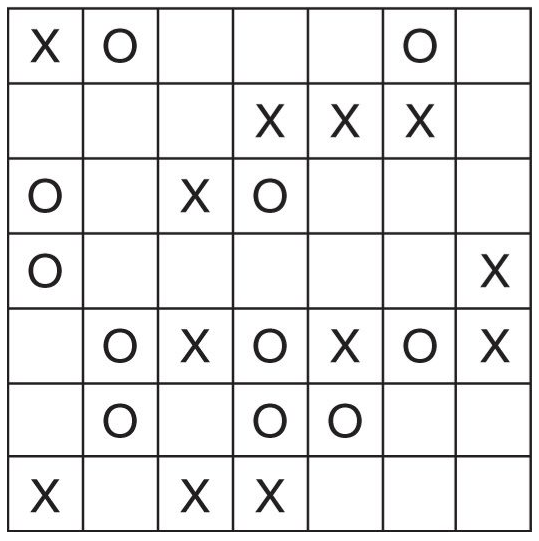
Problem 32
This problem is from the Mensa Page-A-Day calendar for 2015.
Put an X
or O in each empty cell of this grid so that four consecutive X's or O’s do not
appear vertically, horizontally or diagonally.
Click
here for video solution!
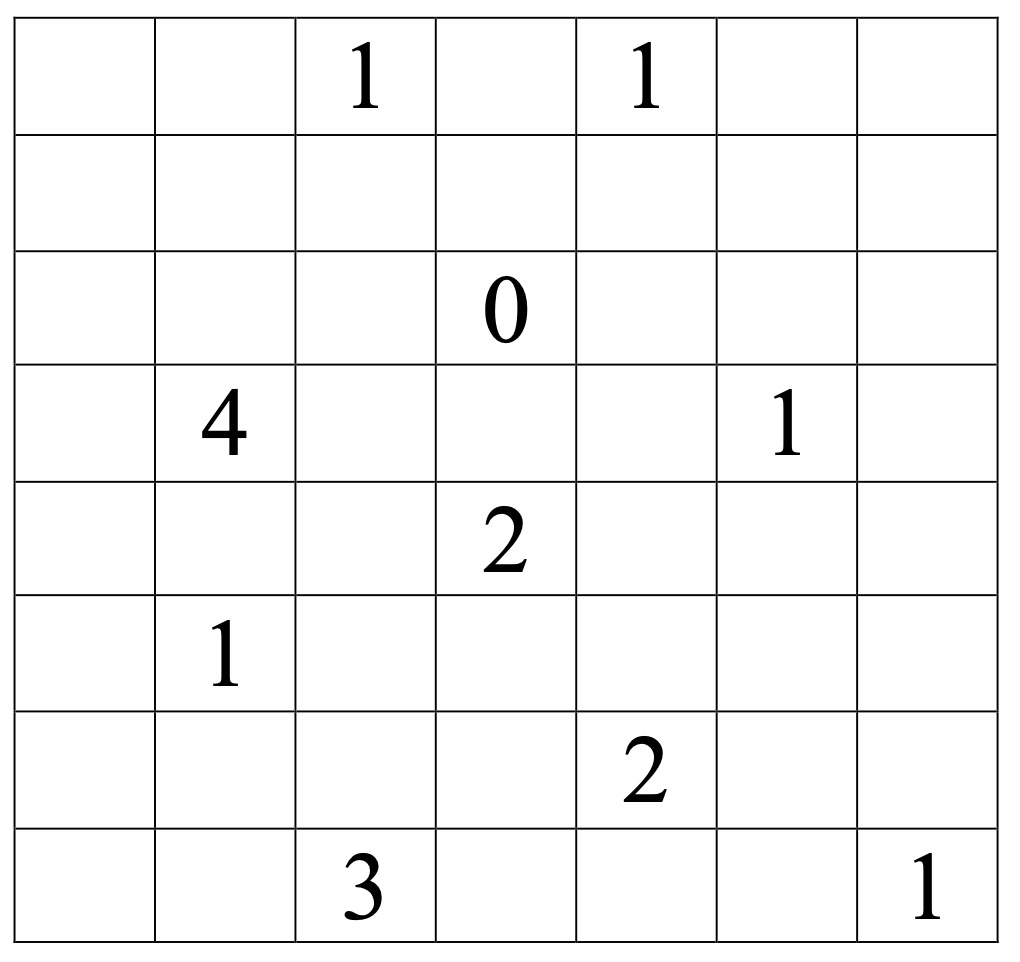
Problem 31
This week’s problem is similar to
one of the puzzles found in the book, The Puzzling World of Winston Breen, by Eric Berlin.
Ten stars have fallen and are hiding
in the grid below. You must find the locations of these stars. A number tells
you how many stars are located next to that cell: horizontally, vertically, or
diagonally. No square with a number in it also contains a star, but a star may
appear in a square with no adjacent numbers. Can you fill in all ten stars?
Click here for video
solution!
Problem 30
A baseball has been placed in a
plexiglass cube so that it may be put on display. The length of the diameter of
the ball and the length of an edge of the cube are equal. The diameter of the
ball in this photo is 2.9 inches. What percent of the volume of the cube is
taken up by the ball? We will accept answers within 2% of the exact answer.
(Problem solvers may look up the formulas for finding the volumes of spheres
and cubes.)

Click
here for video solution!
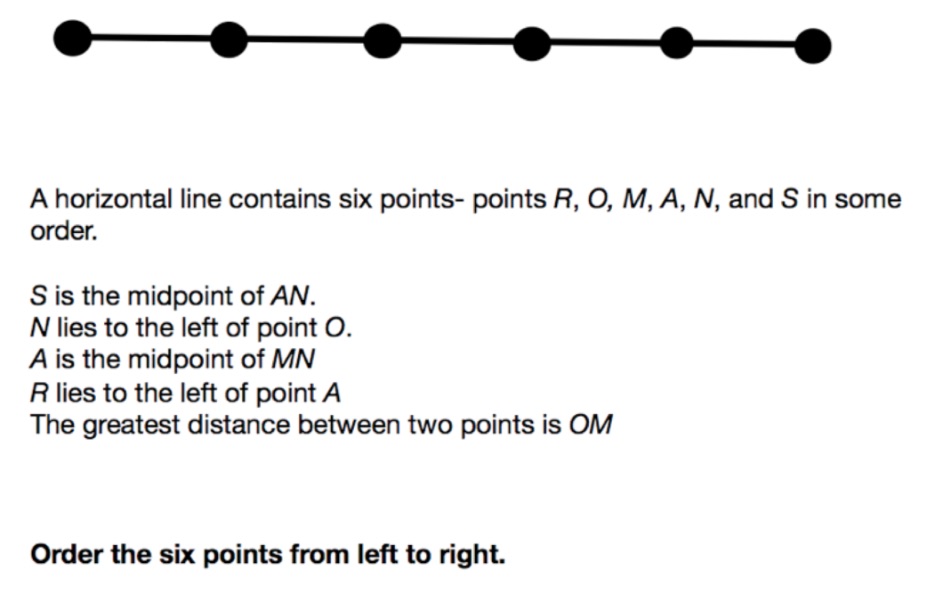
Problem 29
The problem is
another winner in the student video solution contest.
Problem 28
The problem is
another winner in the student video solution contest.
A
pouch contains 3 blue marbles, 4 red marbles and 5 green marbles. You reach
into the bag and remove a marble at random. You put the marble in your pocket
and remove a second marble at random. You put the second marble in your pocket
and remove a third marble at random. What is the probability that your first
marble was red, your second marble was blue and your third marble was green?
Problem 27
The problem is
another winner in the student video solution contest.
Ms.
Hanson is redecorating her house and needs more furniture. The first day, the
furniture she got cost the same as the answer to the problem below:
24 x 7 + 9 – 81 ÷ 3 + 1 x 34
The
second day, the furniture she got cost twice as much as the previous day. The
third day, the furniture she got cost $3 more than the second day. The fourth
day, the furniture she got cost $6 less than the third day. The last day, the
furniture cost one-third less than the fourth day. What is the total cost of
all the furniture she got in the five days?
Problem 26
This problem is another winner in the student video solution contest.
Gary picks a card at random from a standard deck of 52 cards. He puts the card in his pocket and picks another card at random and puts it in his pocket. He does this two more times so that he has a total of four cards in his pocket. What is the probability that all four cards are aces? There are four aces in a standard deck of cards. Write your answer as a simple fraction in lowest terms.


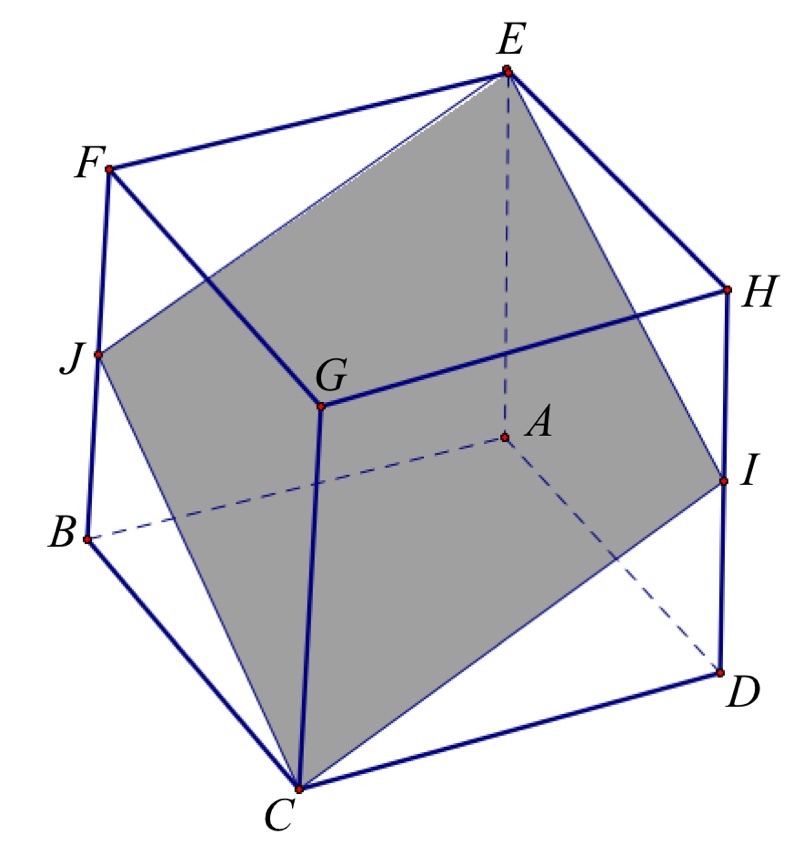
Problem 25
This problem
is the same as POTW #9. The solution given for POTW #9 back in November was
incorrect. The POTW staff member who provided the incorrect solution stated the
shaded area was a square. It is not. It is a rhombus, but not a square. The
correct solution was provided by a student who is another winner in the student
video solution contest.

Problem 24
This problem is another winner in the student video solution contest.
The laughing hyenas live in groups equal to the number that has the greatest probability of coming up as a sum when tossing a pair of standard dice. Laughing lattes live in groups that are equal to the square root of the number of a hyenas in a group to the fourth power. Laughing bees live in groups that are twice as large as the groups of laughing lattes. If there are two groups of hyenas, three groups of lattes and seven groups of bees in an observatory, how many animals are in the observatory?
Problem 23
This problem is another winner in the student video solution contest.
Gary the
Snail has an unknown number of Krabby Patties. The
square of Gary’s number of Krabby Patties is
forty-two more than the number of Krabby Patties that
SpongeBob has. Mr. Krabs has 539 Krabby Patties, and
that number is 3.5 times more than the number of Krabby
Patties that SpongeBob has. Find the number of Krabby
Patties that Gary the Snail has.



Problem 22
. This problem is another winner in the student video solution contest.

Problem 21
This problem is another winner in the student video solution contest.


Problem 20
This problem is another winner in the student video solution contest.

Problem 19
This problem is another winner in the student video solution contest.
Distances are
measured with units of length. Flat surfaces are measured with units of area.
Three-dimensional objects are measured with units of volume. An alternate
universe has six-dimensions. The six-dimensional objects are measured with
units of “sporkle.” What is the “sporkle”
of a six-dimensional hyper-hyper-hyper-cube with a
side length of 2 meters.
Problem 18
This problem is from a Mathematical Olympiad math contest in 2004.
A rectangular floor, 9 feet by 11 feet, is covered completely by
tiles. Each tile is either a 2-foot by 3-foot rectangle or a square 1-foot on a
side. No tiles overlap. What is the least total number of tiles that could have
been used to cover the floor?
Problem 17
This problem is another winner in the student POTW video solution contest.
Find the smallest counting number that leaves a remainder of 4 when
divided by 6, a remainder of 5 when divided by 7, and a remainder of 6 when
divided by 8.
Problem 16
This problem is another winner in the student POTW video solution contest.
A square and a circle have the same area. Each side of the square is 2
inches long. Find the length of the diameter of the circle. Use 3.14 as an
approximation for π.
Problem 15
This problem is another winner in the student POTW video solution contest.
Simplify the expression below:
6÷2(1+2)
Problem 14
Five numbers have a mean (average) of 125, a median (middle number) of
126, and a mode (most frequent score) of 129. What is the sum of the two
smallest numbers?
Problem 13
This problem is from the Mensa 365 Brain Puzzlers Page-A-Day Calendar
Fill in the grid with the names of the eight
U.S. state capitals listed—each six letters in length. One letter is given to
get you started. At the end, rearrange the shaded letters to get another state
capital.
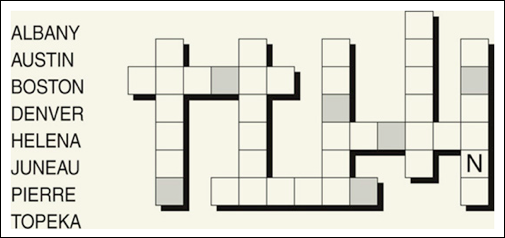
Name of other state capital:
______________________________
Problem 12
This problem is from the 2008 Latin Middle School Math Contest.
Place the integers 1-12 in the circles
so that the sum of the numbers in each of the six rows is 26.
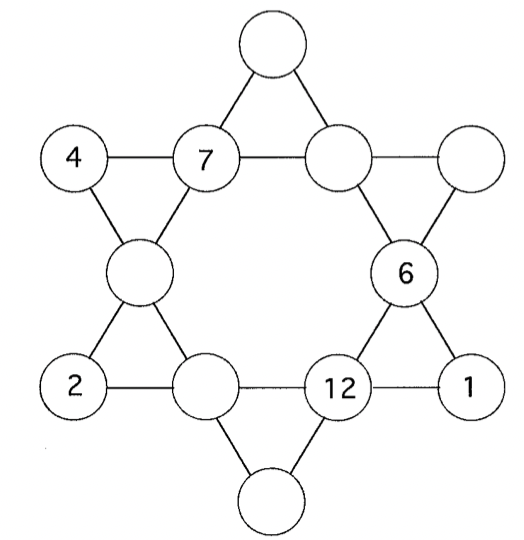
Problem 11
This problem is from the 1998 AMC 8 Math contest.
If the pattern in the triangles below continues, what fraction of the interior would be shaded in the eighth triangle?

Problem 10
This
problem is from the May, 2014, journal, Mathematics Teaching in the Middle School.
Suppose that 18
students took an exam on a day when 4 classmates were sick. When the teacher
handed back the exam, she announced that the mean of the 18 test scores was 74
points. Two days later, after the 4 had taken the exam, she announced that the
mean of the test had risen to 78 points. What was the mean score on the exam
for the 4 sick students?
Problem 9
This problem is from #AMCMATH, maa.org/amc
See Problem 25
Problem 8
Four friends work at a candy factory. Austin
packaged 12 pounds of Halloween candy. Jessica packaged 4 and 4/5 times more
than Austin. Elliott packaged 1/3 less than Jessica. Bridget packaged 2 times
as much Halloween candy as Elliott. One pound of Halloween candy sells for
$12.50. One buyer bought all of the candy that was packaged by the four
friends. How much did that buyer pay?
Click here to view video solution
Problem 7
Nine congruent rectangles are arranged
as shown to form a larger rectangle. The area of the larger rectangle is 720
square inches. What is the perimeter of the larger rectangle?
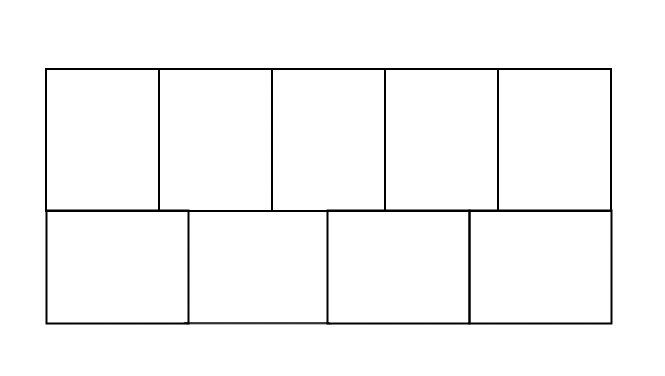
Click here to view video solution
Problem 6
During the recent team mathematics
competition, 6 teams were competing. Each team played each other once, with 2
points for a win, 1 point for a tie, 0 points if they lost. Here are the final
points after all of the matches:
Alices
4
Wooden
Shoes 7
Battling
Bathers 9
Cavemen
5
Pretzels
1
Orphans ?
How many points did the Orphans get?
Click here to view video solution
Problem 5:
This problem was inspired by a problem presented by Dan Meyer at the 2014 NCTM conference in New Orleans.
Write down an addition expression using counting numbers that has a sum of 25. Then find the product of all the counting numbers used to add up to 25. Now find the counting numbers that add up to 25 that have the greatest possible product. You may use as many numbers as you need, and you may use a number more than once. Write the product of the numbers you chose on the paper you hand in.
Click here to view video solution
Problem 4:
Shirley said to Victor, "Say! If you reverse the digits of my age, you get your age." Then Victor said to Shirley, "Nine years ago I was twice as old as you were." How old are Shirley and Victor now?
Click here to view video solution
Problem 3:
This problem is from the Mensa 365 Brain Puzzlers Calendar for 2014
In this magic square, every row, every column, and
both main diagonals add up to the same value, which you must determine. There
is only one way to complete the square. Write counting numbers in the six blank
squares to complete the magic square.
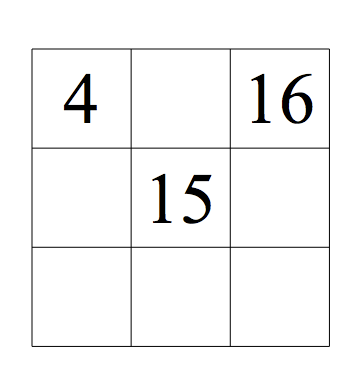
Click here to view video solution
Problem 2:
This problem is from the 1984 middle school math contest hosted by the Prairie School.
A picture is 6 inches by 8 inches. Carol wants to
put a border 2 inches wide all around the picture. How many square inches of
cardboard does she need for the border? See the drawing please.
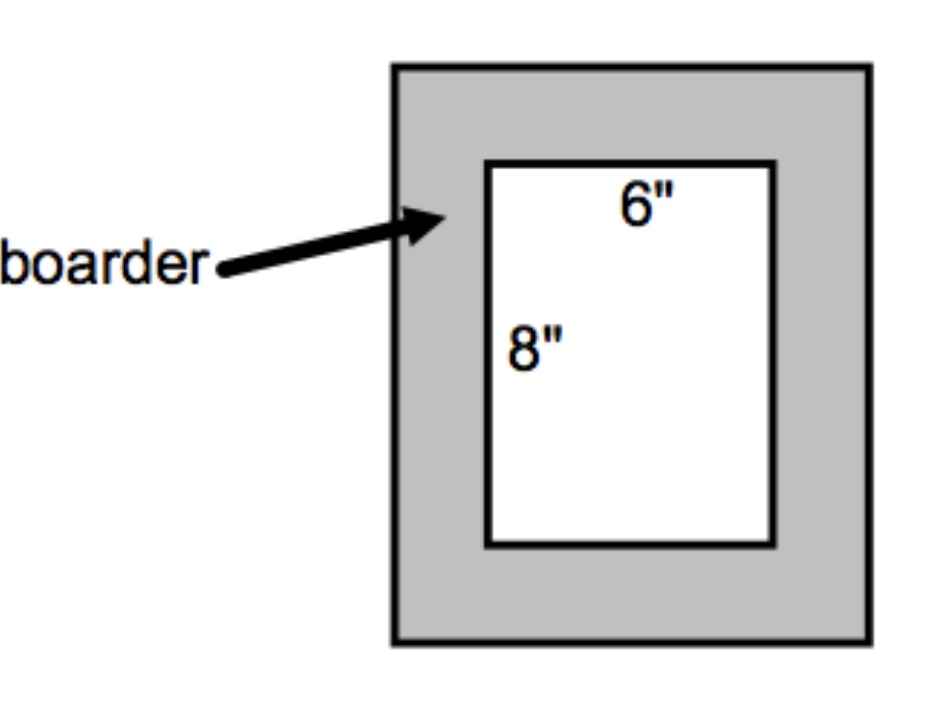
Click here to view video solution
Problem 1:
This
problem is from the brainbashers.com website.
The BrainBashers safe has a rather
unusual control panel.
In order to open the safe you have to press every single button once only, in the correct sequence, ending on the
button marked E.
Each button clearly states which button to press
next, for example, 2U means move up 2 buttons and 3R means move right 3
buttons.
Can you determine which button you must start
with?

Click here to view video solution.