Click here for 13
more years of problems
LSC MS POTW
2020-21 School Year
Scroll down for earlier problems
This is the final problem for the 2020-21
school year. We will be back next fall for the 15th year of weekly
problems.
Problem 34:
This problem comes for the Art of
Problem Solving Prealgebra Book
In how many ways
can you spell the word NOON in the grid below? You can start on any letter,
then on each step you can move one letter in any direction (up, down, left,
right, or diagonal). You cannot visit the same letter twice in each spelling of
NOON.

Click here
to watch video solution.
Problem 33:
The problem below is another winner of the POTW student video
solution contest.
The length of the rectangle below is twice as long as the width.
The diagonal from X to Z is ![]() units long. What is the area (in square units)
of triangle XYZ?
units long. What is the area (in square units)
of triangle XYZ?

Click here to watch video
solution
Problem 32:
The
world’s unluckiest golfer’s ball sits 20-feet from a hole. He can only putt 3,
5, 7, or 11 feet at a time. This golfer is unlucky, because whenever he aims
one of his putts directly at the hole from a distance closer than the length of
the putt, the ball bounces over the hole. His ball only goes in the hole when
he putts from exactly 3, 5, 7, or 11 feet away. What is the least number of
putts he can take to get the ball in the hole?
Click here
to watch video solution.
Problem 31:
Harold
has a bag of gummy bears containing 104 gummy bears. Harold gave 25% to his twin,
Gerald. He also gave 13 to his mom. Finally, he gave 1/13 of the remaining
gummy bears to his sister, Stacy. How many did he have for himself?
Click here
to watch video solution.
Problem 30:
Harry, Hermione, and Ron
played a game with marbles. The winner of each round of the game got from each
of the other players as many marbles as the winner had at the start of that
round. After Round 2, Harry had 5 marbles, Hermione had 6, and Ron had 7. How
many marbles did Harry have at the start of the game?
Click here
to watch video solution.
Problem 29:
A
bat and a ball cost one dollar and ten cents total. The bat costs a dollar more
than the ball. How much does the ball cost?
Click here
to watch video solution.
Problem 28:
How
many children are there in a family in which each boy has as many sisters as
brothers but each girl has twice as many brothers as sisters?
Click here
to watch video solution.
Problem 27:
This week’s problem comes from the Page-a-day
Mensa Puzzle calendar for 2021
Choose two
consonants and repeat them as many times as needed to complete this crisscross
puzzle. All vowels have already been placed. Create uncapitalized words
commonly used in English. No words may be repeated. Latin School students
should turn in an answer by typing the word from the puzzle that is most
closely association with math.

Click here to watch video
solution.
Problem 26:
Special, longer problem for Spring Break!
A ten-digit number meets the following requirements.
Each digit is different. Starting from the left, the first digit makes a number
evenly divisible by one. The first two digits make a number evenly
divisible by two. The first three digits make a number evenly divisible
by three, and so on until the entire ten-digit number is evenly divisible by
ten. What is the number?
Click here to watch video
solution.
Problem 25:
This problem in honor of Pi Day, March 14, 2021!

PI does not stand for P times I in this puzzle. It represents a 2-digit
number with P in the tens place and I in the ones place. PIE stands for a
3-digit number with P in the hundreds place, I in the tens place and E in the
ones place.
Click here to watch video
solution.
Problem 24:
The binary number
1111110001, which equals the hexadecimal number 3F1, when converted to Roman
numerals, spells what English word? It is one of the very few common words
which are valid Roman numbers.
Click here to watch video
solution.
Problem 23:
This
problem is from the third annual Latin School of Chicago Middle School Math
contest, “2002: A Mathematics Palindrome,” on Feb. 9, 2002.
An
unusual dartboard is shown below. Each dart scores 5 points, 12 points, or 21
points. Suppose you can throw as many darts as you like, and your score is
determined by adding all the 5’s, 12’s, and 21’s together. Choosing from the
set of counting numbers, find the largest score that is impossible to obtain.

Click here to watch video
solution.
Problem 22:
Brick
masons are going to build a decorative brick wall at a school. The bricks will
be stacked on the top of one another. The bricks will be placed so that each
row of bricks will have 1 fewer brick than the row below it. If the masons are
going to use 105 bricks and want only 1 brick block on top of the wall, how
many bricks will need to be in the bottom row?
Click here to watch video
solution.
Problem 21:
Arrange
four 9's and use a maximum of two math symbols to make an expression equal to
100.
Click
here to watch video solution.
Problem 20:
There are two horses in a race starting at different times. The 1st horse starts at 10 p.m., and the 2nd horse starts at 2 a.m. the next day. The first horse runs 6 miles per hour and the second horse runs 10 miles per hour. At what time will the second horse catch up to the first horse? (Be sure to include AM or PM)
Click
here to watch video solution.
Problem 19:
A
bag contained 80 marbles, and 80% of them were blue and the remainder were
orange. Some of the blue marbles were removed from the bag and after this, 60%
of the marbles in the bag were blue. How many blue marbles were removed from
the bag?
Click here to watch video solution
Problem 18:
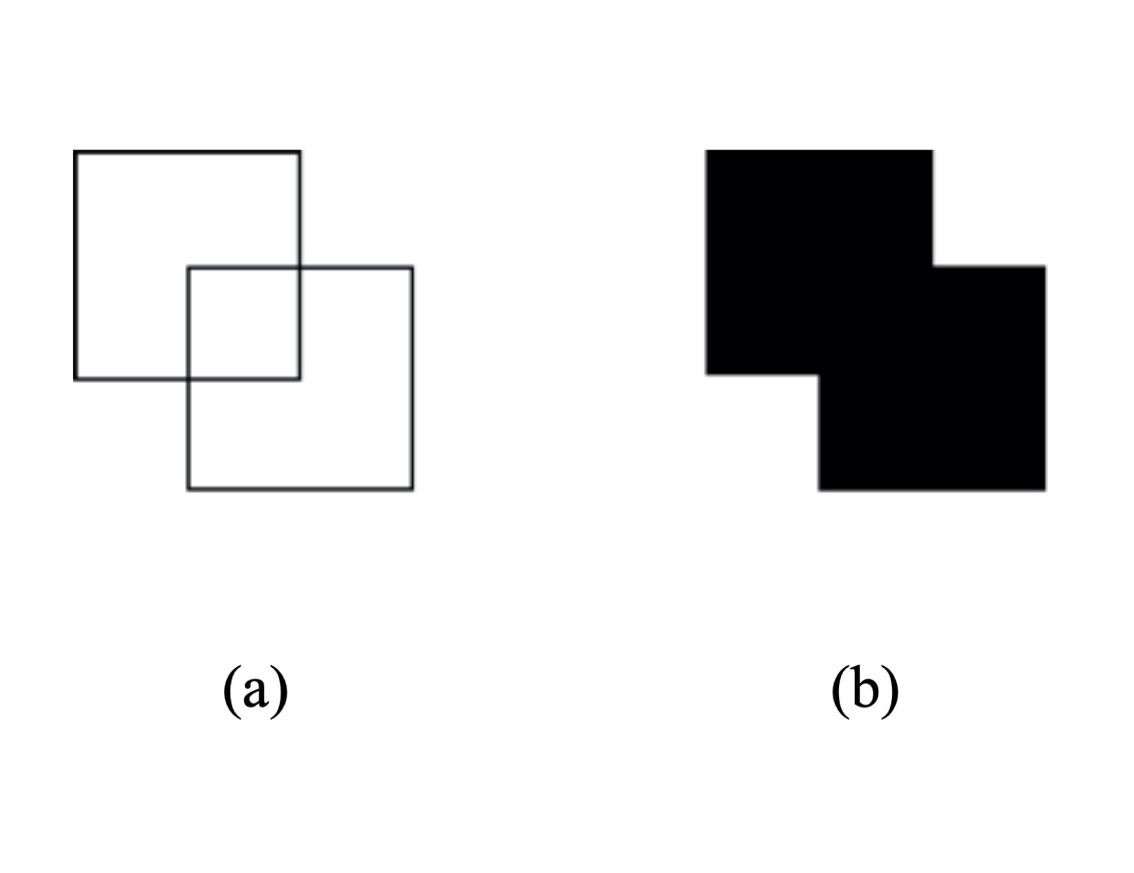
Roma draws one square and then draws another square of the same size. The two squares overlap, as shown in (a), in such a way that the tiny square formed by their overlap has an area that is exactly one-fourth the area of each of the two original squares. If Roma fills in the interiors of all the squares, the resulting figure, shown in (b) has an area of 567 square centimeters. What is the perimeter of figure (b)?
Click here for video
solution.
Problem 17:
Roman bought a bag of candy. He gave
away ten percent of the candy to his sister and then gave three pieces to his
brother. He gave one-fourth of what was left to his grandmother and then ate
one- half of the remaining eighteen pieces of candy. How many pieces of candy
were originally in the bag?
Click here for video
solution.
Problem 16:

Click
here for video solution.
Problem 15:
The Twins-R-Us day care
center only accepts pairs of twins. Recently the center had 35 sets of twins
enrolled. Of the total number of children, 38 were boys, and there were four
more sets of girl-girl twins than of girl-boy twins. How many sets of boy-boy
twins were enrolled?
Problem 14:
People celebrate in many different ways this time of
year, and cookies are a part of many celebrations. Clyde baked some cookies and
then gave them to each of his three sisters.
To the oldest, he gave half of the cookies and half a cookie. He then gave half of what was left and half a
cookie to his second sister. Finally, he
gave half of what was then left and half a cookie to his youngest sister. He then had one cookie left, and he ate
it. At no time was a cookie broken or
cut. How many cookies did Clyde bake to
begin with?

Problem 13:
This problem is from the 2011 Mensa Puzzle Page-A-Day Calendar from Workman Publishing.
Harry
had a bag of Bertie
Bott's Every Flavor Beans. He gave half of his beans to Ginny, one-fifth of them to Ron, and one-sixth
to Hermione. He kept 8 beans for himself. How many beans were in the bag
originally?

Problem 12:
This problem is the first winner
for 2020-21 of the student video solution contest.
![]() x
x ![]() = 30
= 30
![]() – 2 =
– 2 = ![]()
4
+ ![]() = 24 –
= 24 – ![]()
60
÷ ![]() =
= ![]() x 2
x 2
![]() –
– ![]() =
= ![]()
![]() x (
x (![]() ÷
÷ ![]() )
–
)
– ![]() = ?
= ?
Problem 11:
Katniss
can run 5-kilometers in 18 minutes. Gale can run 5-kilometers in 21 minutes.
How many minutes will it take Gale to run a race that takes Katniss 45 minutes
to complete, and how many meters long is the race?
Gale's
time for race: ________ minutes
Length of race: __________meters
Click
here for video solution.
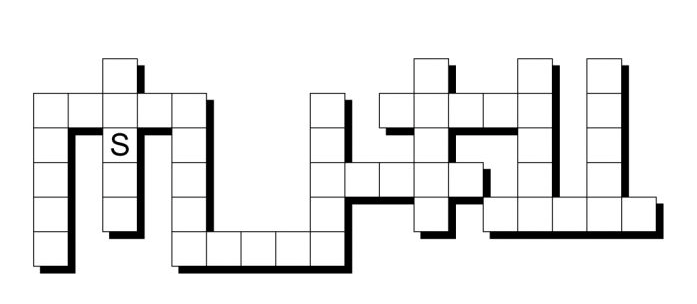
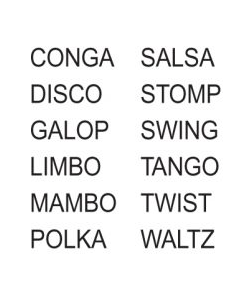
Problem 10:
This problem from the Mensa 365 Brain Puzzlers — 2015 Page-A-Day Calendar.
Fill in the grid with the names of twelve 5-letter
types of dances. One letter is given to get you started.
Problem 9:
This week’s problem comes from the Brainbashers website.
A library decided to hand out
some of its old books to the 1,400 people who lived in the town. To each
library member they offered 6 books, and to each non-member they offered 4
books. If only half of the members, and three quarters of the non-members, accepted
the books, how many books were given away?
Click
here for link to video solution.
Problem 8:
The
letter, I, is formed by placing three 5 cm by 12 cm rectangles next to each other,
as shown. None of the rectangles overlap. What is the perimeter of the I?

Click
here for video solution.
Problem 7:
A
baseball minor league consists of two 6-team divisions. Each team plays every
other team in its division N games at home and N games away. In addition each team plays every team in the other division M
games at home and M games away, with N > M > 1. Each
team plays a 108-game schedule. Find the number of games a team plays within
its own division.
Problem 6:
Two
different scales are used to measure loud noises. The "Big Bang"
scale reads 42 when the "White Noise" scale reads 0. The "Big
Bang" scale reads 127 when the "White Noise" scale reads 50. The
noise made when a book fell to the floor registered 65 on the "Big
Bang" scale. To the nearest whole number, what would that noise have
registered on the "White Noise" scale?
Problem 5:
Tris saw an ad for a sweater on sale. The ad read "$50, less 10%." The next week the store reduced the previous week's sale price by 20%. Tris ran to the store, found the sweater, and to her delight, right by the sweater was a sign that read, "an additional $8 off." At the checkout they give her 10% off because was it was Flashback Friday. Tris had to pay 8.5% sales tax. To the nearest cent, how much did Tris pay for the sweater?
Problem 4:
This problem is from the 2008 Latin Middle School Math Contest.
Place the integers 1-12 in the circles so that the sum
of the numbers in each of the six rows is 26. Submit your answer in the Google
form by typing just the integer that belongs at the very top.

Problem 3:
This
problem is from the Mensa 365 Brain Puzzlers — 2015
Page-A-Day Calendar
Nine knights—numbered 1 through 9—are to be seated facing the
Round Table in such a way that every knight's number is at least 3 higher or
lower than the knight's number immediately adjacent on the right and left.
Additionally, the sum of the two knights facing each other at the ends of the
line painted across the table sums to an even number. With knights 2, 6, and 8
seated as shown, seat the rest of the knights. Submit your answer by starting
with the 6th knight and writing the knights’ numbers in clockwise
order.

Problem 2:
This week’s problem
comes from Mr. Jason Koza. He taught 7th grade math
at Latin during the 2013-14 school year. He now teaches math at Colorado
Academy in Denver Colorado.
Kristiana
has a 10 yard by 25 yard pool. The pool is filled to a
depth of 2 yards. If she has a pool party and 10 people jump in, they will
displace 50 cubic yards of water. What is the new depth of the pool with the 10
people?
Click
here for video solution!
Problem 1:
A magician had a bag that doubled the amount of money put into it. She agreed to allow a man to borrow the bag if the man gave the magician $16 after each doubling. Each time that the man used the bag, he put in all the money he had; but after the fourth time that he used the bag and paid the magician, his money was completely gone. With how much money did he begin?
Click here for video
solution!