Click here for 14
more years of problems
LSC MS POTW
2021-22 School Year
Scroll down for earlier problems
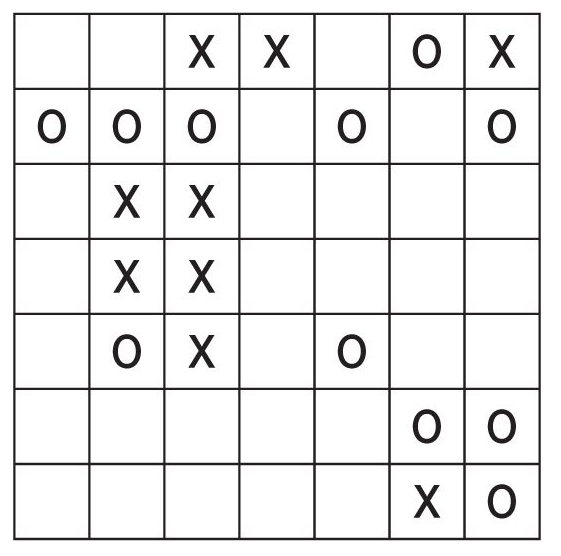
Problem 33:
(This if the final problem of the 21-22 school year)
This problem is from the 2017 Mensa Page-A-Day puzzle calendar.
Put an X or O in each empty cell of this grid so that four consecutive X's or O's do not appear horizontally, vertically, or diagonally.
Click here for video
solution.
![]()
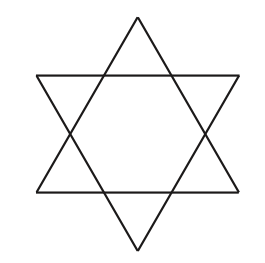
Problem 32:
A unit hexagram is composed of a regular hexagon of side length 1 and its 6 equilateral triangular extensions, as shown in the diagram. What is the ratio of the area of the extensions to the area of the original hexagon?
Click here for video
solution.
Problem 31:
How many squares of any size can be formed by connecting dots in the 4x4 grid
shown?

Click
here for video solution.
Problem 30:
If
the mean, median, and mode are all equal for the set
{3,
4, 5, 8, x}, what is the
value of x?
Click here for video
solution.
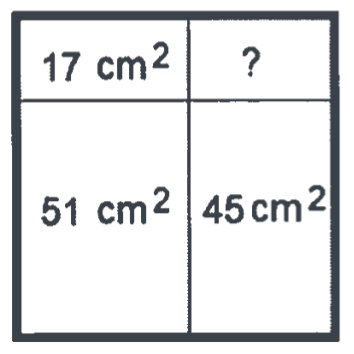
Problem 29:
This problem is from the 7th grade Noetic Learning spring contest for 2022.
Solutions may be submitted by email to: tcanright@latinschool.org
In the picture below, a rectangle is divided into 4 smaller
rectangles by two lines. The areas of 3 of the smaller rectangles are given in
the picture. What is the area of the smaller rectangle with the question mark?
Note: The figure is not drawn to scale.
Click here for video solution.
Problem 28a:
This problem is a special edition POTW for "4 @ 45".
This problem is from the November, 2004, Mathematical Olympiads monthly math contests
Elsa, Anna, and Merida play in the school
band. One plays the flute. One plays the saxophone. One plays the drums. Elsa
is a 4th grader. Elsa and the saxophone player practice together after school.
Anna and the flute player are 5th graders. Who plays the drums?
Click here for video
solution.
Problem 28b:
This problem is a special edition POTW for "4 @ 45".
Roman and Caesar love riding bicycles. One day they
planned a long bike ride. Roman knew that he would average twenty-five miles
per hour and Caesar would average fifteen miles per hour. Roman said to Caesar,
"I will give you a three hour head start, and
then we will end our rides when I catch up to you." Caesar said,
"fine," and he began his ride. Roman took a nap. Three hours later
Roman was still asleep so he did not actually begin his ride until Caesar had a
three hour and twenty minute head start. How many
miles had each cyclist ridden when Roman caught up to Caesar?
Click here for video
solution.
Problem 27:
This problem is from the 2012 Page-A-Day Mensa 365 Brain Puzzlers calendar.
A palindrome reads the same backward and forward. What seven-digit palindromic number satisfies all of the conditions below?
1. No
digit appears more than twice.
2. Zero is not used.
3. The last digit is three times the amount of the second digit.
4. The third digit minus the sixth digit = the middle digit.
5. The sum of all the digits = 41.
Click here for video
solution.
Problem 26:
This problem is from the Mensa 365 Brain Puzzlers — 2017 Page-A-Day Calendar
Each of the six letters stands for a different counting number from 1 through 9. Using the four clues, can you deduce the number represented by each letter?
• The sum of the three
numbers in each row is 14.
• Each of the three numbers
in the top row is a perfect square.
• C, D, and E are consecutive counting numbers in increasing order.
• A is larger than B.
Click here for video
solution.
Problem 25:
Colored beads are placed in the
following order: 1 red, 1 green; then 2 red, 2 green; then 3 red, 3 green; and
so on. In all, how many of the first 100 beads are red?
Click here for video
solution.
Problem 24:
This
problem is in honor of Pi Day, March
14.
We followed the Pied Piper down the turnpike from Pittsburgh where the Pirates play baseball to Mississippi to work on this problem.
While in Mississippi we went
to a wildlife park where we observed piglets, porcupines, pileated woodpeckers, pike, and pigeons. We then drank a pint of Pibb Xtra and ate pita bread and spanakopita
while thinking about traveling to Pisa,
Italy. We went to Pierre,
South Dakota instead, because the Philippines
was too far away. There we met up with Pippi Longstocking who shared this
problem about pizza pie.
Pippi purchased a round pizza that was twenty-four inches in
diameter. She then cut the pizza in half. Next, she cut one of the two
pieces into thirds.
Finally, she took one of the newly cut pieces and cut it into four equal pieces. She then ate one of the pieces she had just cut. What was the area
of that piece? You may answer
in terms of pi, or you may round
your answer to the nearest tenth of a square inch.
Click here for video solution.
Problem 23:
This
week’s problem is another winner in the student POTW video solution contest.
Suzy
and her friend are buying Saint Patrick’s Day items. Suzy buys 3 leprechaun
hats and one green shirt. She ends up paying $9. Her friend pays $19 for 2
leprechaun hats and 5 green shirts. How much do leprechaun hats cost?
Problem 22:
This week’s problem is from the book, Math with Bad Drawings, by
Ben Orlin.

Write the dimensions of the two rectangles.
First rectangle:
Length = _______ Width = ______
Second rectangle:
Length = ________ Width = _______
Problem 21:
This
week’s problem is from the film,
Little Big League. Joe can paint a house in three hours, and Sam
can paint a house in five hours. How long will it take them to paint the house
if they work together?
Problem 20:
This problem is from the 2013 Mensa Page-A-Day calendar.
For
a giant yoga demonstration, each yoga studio was going to send 14 people to
participate. However, three studios backed out, and the remaining studios each
sent seven more people to make up the difference. How many yoga studios were
originally going to send people to the demonstration?
Problem 19:
This
week’s problem is another winner in the student POTW video solution contest.
Joe is playing a word game where vowels
are worth a prime number of points. The worth of vowels is more than 5 and less
than 11. The letter D is worth twice as much as vowels, and the letter S is
worth the sum of the worth of the letter D and the worth of a vowel. To get the
worth of the letter T add 9 to the worth of the letter S, then divide that sum
by 10. The letters C, B, and R are all worth one less
than the worth of the letter S. If Joe plays the words ADD and SUBTRACT, how
many points will Joe earn for the two words combined?
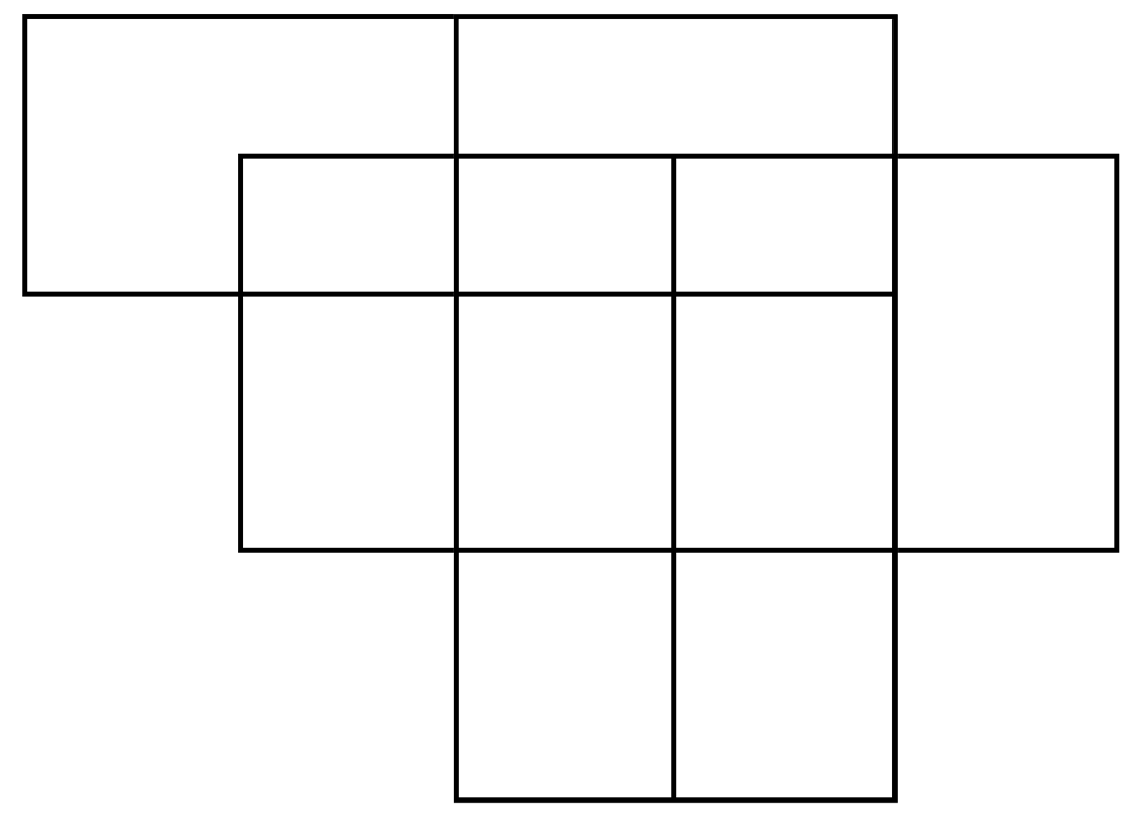
Problem 18:
This problem is from the 2012 Page-A-Day
Mensa 365 Brain Puzzlers calendar.
How many rectangles of all sizes are
formed by the lines in this diagram?
Problem 17:
This
week’s problem is another winner in the student POTW video solution contest.
Steve, Tony, Peter, Natasha
and Scott have each taken a math test. The average of their scores was 83. Four
of the scores were 83, 92, 76 and 85. What was the last score?
Problem 16:
This week’s problem is from the “Page-A-Day” Mensa Puzzle Calendar for 2022.
The longest word in the Dr. Seuss book Green Eggs and Ham,
and the only word containing more than one syllable, can be formed by
rearranging eight of the letters in the phrase HAPPY NEW YEAR. What is that
word?
Problem 15:
This week’s problem is from the “Page-A-Day” Mensa Puzzle Calendar for 2011.
Thirteen books–three red (R), four orange (O), one yellow (Y), three green (G), and two blue (B)–are positioned side by side on a bookshelf. The positions are numbered consecutively 1 to 13. Also: The four orange books are evenly spaced two positions apart, and their four position numbers total 36. The blue books have three books between them. Exactly two red books are next to each other. Neither is at an end. The yellow book is the only book between an orange and a green book. One red book and one green book are at either end.
What is the order of the books?
___ ___ ___ ___ ___ ___
___ ___ ___ ___ ___ ___ ___
1 2
3 4 5
6 7 8
9 10 11
12 13
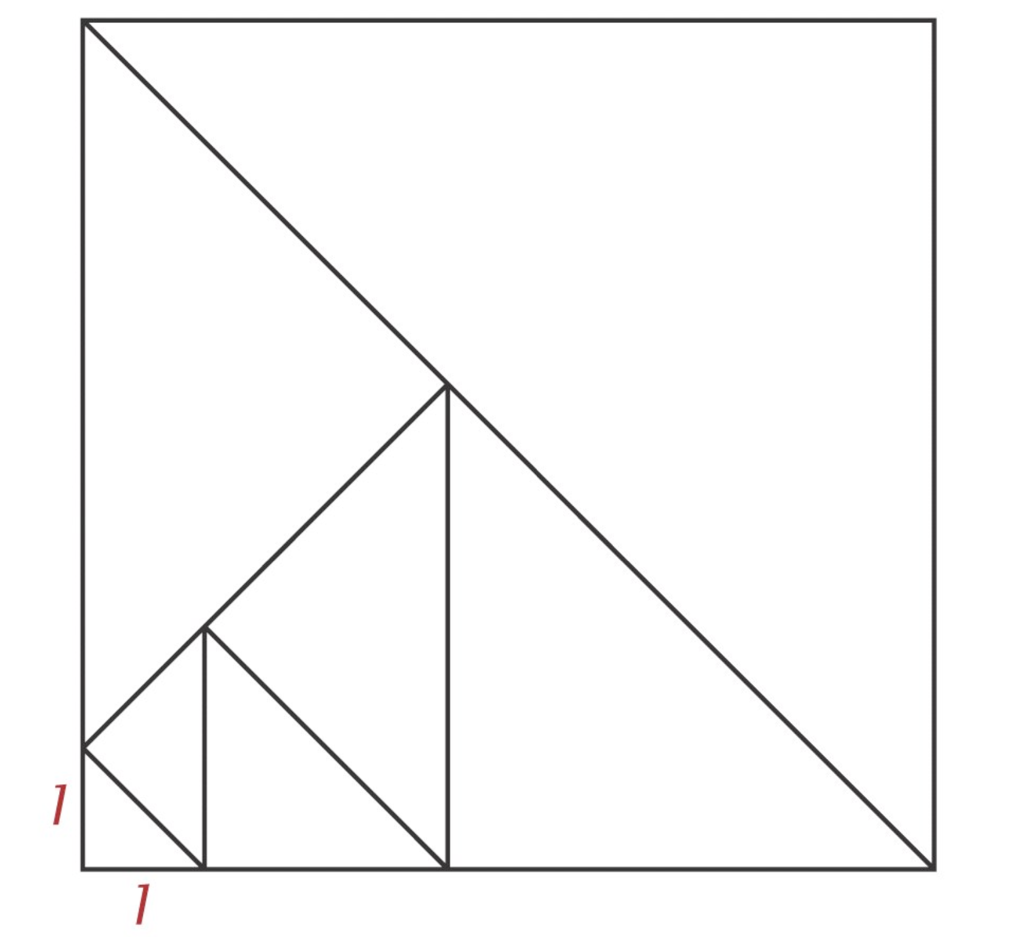
Problem 14:
Find the perimeter of the square. All
triangles are isosceles right triangles.
Problem 13:
A player in the game of Globnor can score 3 or 5 points each round. At the end of a
game a player has scored 79
points. How
many possible ways are there to score 79 points playing Globnor?
Problem 12:
Create a word ladder
from GIVES to THANK. (BONUS: What is the shortest word ladder you can make?)
A word ladder changes one letter at each
rung in the ladder while preserving a word each time. Here is an example of a
word ladder from DOG to CAT.
DOG
COG
COT
CAT
Problem 11:
The 100-Meter-Dash Puzzle
We look at
another challenging math problem listed in the book, In Code, by Sarah
Flannery.
Albus, Severus, and Minerva ran a 100-meter dash. Each ran at a uniform speed
throughout. When Minerva crossed the finish line to win the race, she was
10-meters ahead of Albus. When Albus crossed the finish line to finish second,
he was 10-meters ahead of Severus. How many meters was Minerva ahead of
Severus, when Minerva crossed the finish line?

Click here for video solution.
Problem 10:
The Insurance Man
Puzzle
This
puzzle is the favorite puzzle of Sarah Flannery, the author of the book, In Code.
An insurance salesman knocks on the door of a home in a housing development. When a lady answers he asks, “How many children do you have?” She replies, “Three.” When he asks, “What are their ages?” she decides that he is too cheeky and refuses to tell him. After he apologizes for his apparent rudeness he asks for a hint about the children’s ages. She says, “If you multiply their three ages you get 36.” (Their ages are exact numbers.) He thinks for a while and then asks for another hint. When she says, “The sum of their ages is the number on the house next door,“ he immediately jumps over the fence to determine this number. This done, he returns to the lady and asks for one last hint. “All right,” she says, “the eldest plays the piano!” He then knows their ages. Do you?

Click here for video solution.
Problem 9:
Hogwart’s Professor of
Arithmancy, Septima Vector, has an unusual pair of
dice. Each die is a standard 6-sided cube, but the six faces bear the first six
numbers of the Fibonacci sequence, 1, 1, 2, 3, 5, and 8. If this pair of dice
is rolled once, what is the probability that the sum of the numbers showing on
the top faces of the two dice is a Fibonacci number?
Click here for video solution.
Problem 8:
If
3 smiles
=
10 grins
and
6 grins
=
9 laughs, how many laughs does it take to
equal 2 smiles?
Click here for video solution.
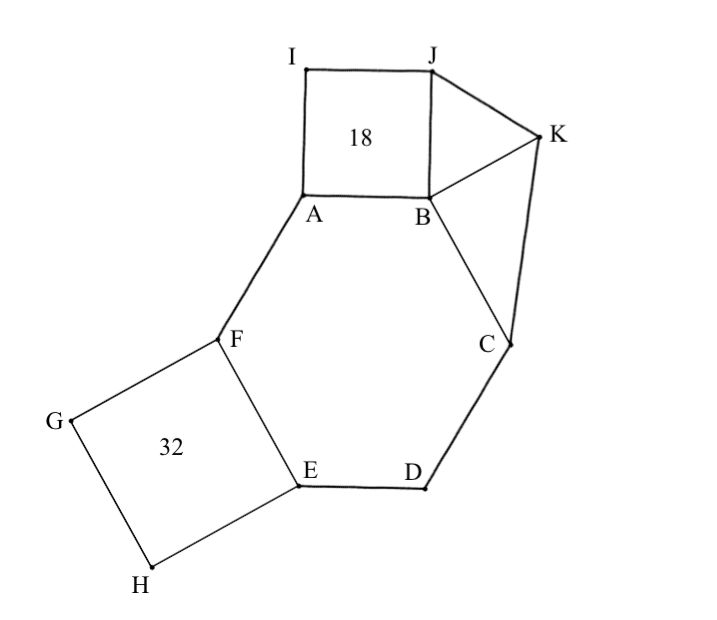
Problem 7:
In the given figure hexagon ABCDEF is equiangular.
Polygons ABJI
and
FEHG
are
squares with areas of 18 and 32 respectively. Triangle JBK is equilateral
and FE
= BC. The
measure of each interior angle of an equiangular hexagon is 120º. What is the
area of triangle KBC?
Click here for video solution.
Problem 6:
A magician had a
bag that doubled the amount of money put into it. She agreed to allow a man to
borrow the bag if the man gave the magician $16 after each doubling. Each time
that the man used the bag, he put in all the money he had; but after the fourth
time that he used the bag and paid the magician, his money was completely gone.
With how much money did he begin?
Click here for video solution.
Problem 5:
Four singers
take part in a musical round of four equal lines, and each sings the round through
three times continuously. SpongeBob starts singing and is followed by Sandy, Squidword, and Patrick, respectively. Sandy starts singing
when SpongeBob begins his second line, Squidword
starts when SpongeBob begins his third line, and so on. For what percent of the
total singing time are the four singing simultaneously?
Click here for video solution.
Problem 4:
There
are two doors; one takes you to freedom and one leads to your eternal
imprisonment. There is a guard guarding each door. One guard always lies, and
one guard always tells the truth. You do not know which door is which, or which
guard is which. You may only ask one guard one question. What question will
allow you to figure out which door is which?
Click here for video solution.
Problem 3:
This
problem is from the Mensa 365 Brain Puzzlers — 2016
Page-A-Day Calendar
Mabel is making a homecoming mix using orange,
dark blue, and light blue chocolate candies. She has 128 light blue candies and
wants this to be 32% of the mixture. She also wants the same number of orange
and dark blue candies in the mixture. How many orange candies should Mabel
include?
Click here for video solution.
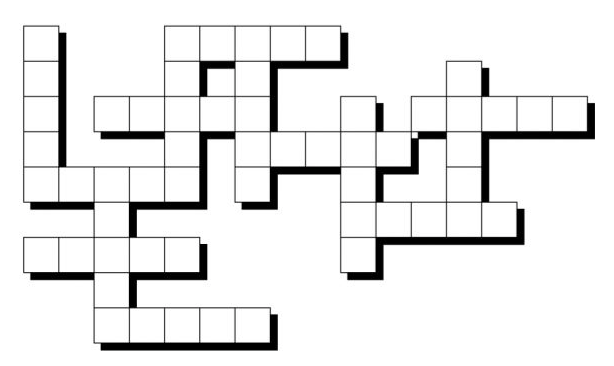
Problem 2:
This
problem is from the Mensa 365 Brain Puzzlers — 2016
Page-A-Day Calendar
Fill in the grid with the last names of 14 Oscar winners for
Best Actress, with each last name five letters in length. The names are listed
below: BATES, BERRY, DAVIS, FIELD, FONDA, HAYES, KELLY, LANGE, LEIGH, LOREN,
SMITH, SWANK, TANDY, YOUNG
 Click here for video
solution.
Click here for video
solution.
Problem 1:
This week’s problem comes from the
Mensa Page-A-Day calendar for 2020-21.
In
this addition problem, each digit has been replaced with the same letter
everywhere it appears, and no two letters stand for the same digit. None of the
three numbers starts with zero. Try to find the unique solution.

Click here for video solution.