Click here for 16
more years of problems
LSC MS POTW
2023-24 School Year
Scroll down for earlier problems
Comments? tncanright@gmail.com
The POTW has concluded for the 2023-24 school
year. We hope to be back in September, 2024
Problem
34:
Use the numbers 1-100 to make the longest chain.
A number is added to the chain if it is a factor or a multiple of the number
that precedes it. 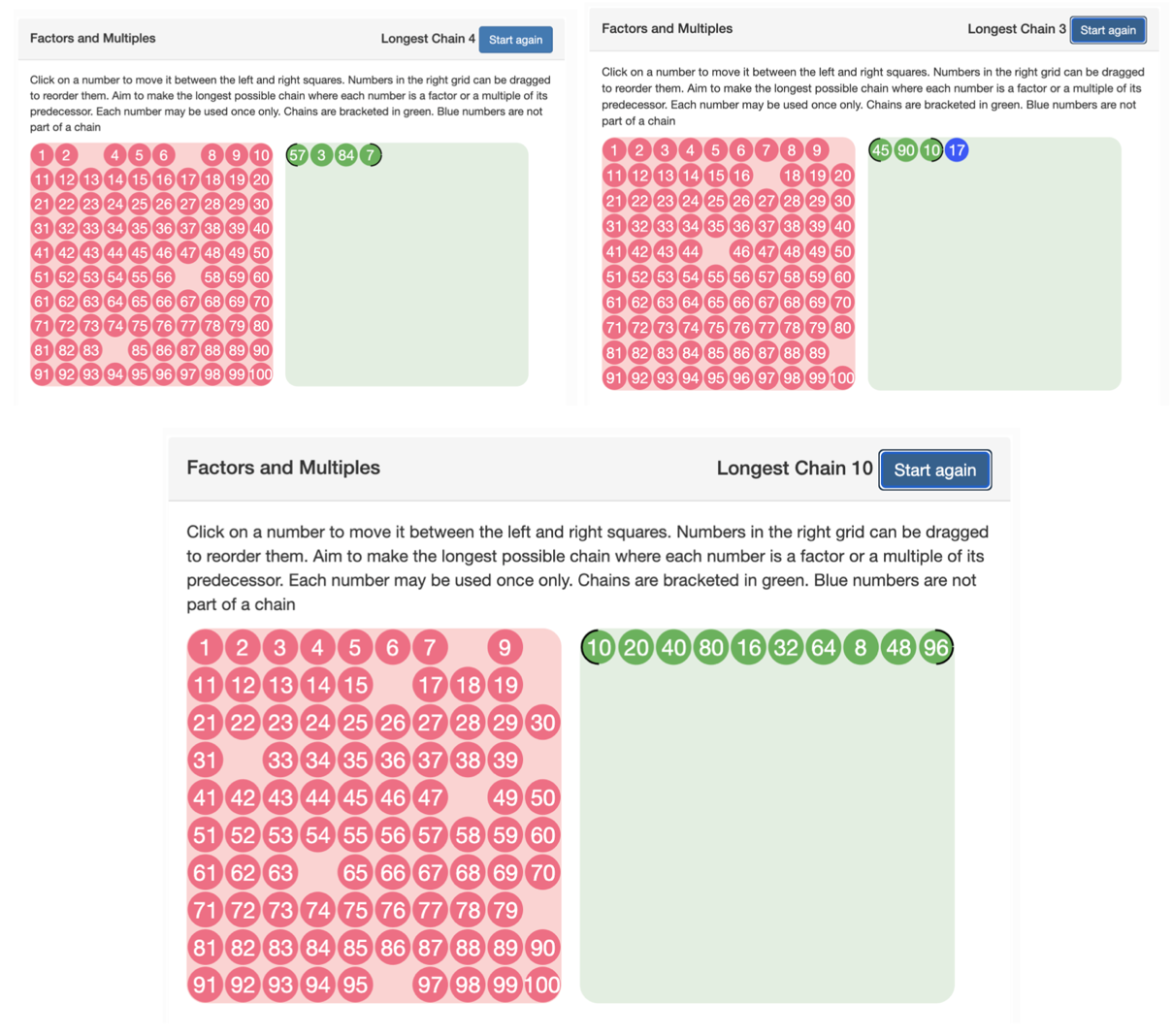
(Here is the link to the online platform: https://nrich.maths.org/factorsandmultiples)
Problem
33:
Nikola Jokic (aka the Joker) won the 2024 NBA MVP,
earning 926 award points. These points are awarded based on votes from a panel
of 99 judges and reporters.
Each judge gets one 1st, 2nd, 3rd, 4th, and 5th place vote. First place votes
are worth 10 points.
Second place votes are worth 7 points.
Third place votes are worth 5 points.
Fourth place votes are worth 3 points.
Fifth place votes are worth 1 point.
(Note: A judge must choose five different players for their ballot.)
What fraction of the total award points given did the
Joker receive? (Please give your answer in a simplified fraction.)
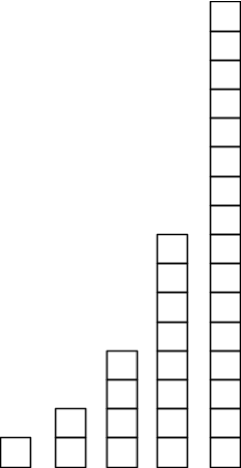
Problem
32:
How many different heights of towers can you make from stacking the 5 pieces below? (All towers must be 1 square wide.)
Problem
31:
A rectangle has whole number side lengths and an area
of 126.
What is the sum of all possible different perimeters of the rectangle?
Problem
30:
Here is how to play the game of wipeout!
(N stands for the amount of numbers.)
Example: ● N=6
● One of the numbers 1-6 is “wiped out”
● The
mean (average) of the remaining numbers is 3.2
The goal is to figure out which number was wiped out. Answer: 5 was wiped out because (1 + 2 + 3 + 4 + 6)/5 = 3.2
One of the numbers 1 to N is wiped out. The mean of
the numbers that are left is 20.75. Which number was wiped out?
Problem
29:
This week’s problem is for 4@45
The summer of 2024 is a double emergence of two
broods of cicadas. Brood XIII emerges every 17 years and Brood XIX emerges
every 13 years. The last time both broods emerged before 2024, the Louisiana
Purchase happened! What year will both broods next emerge together?
Problem
28:
The problem below is another winner of the POTW student
video solution contest.
Find a 10 digit number that describes itself.
That is, the first digit will be the number of 1’s in the number, the second
digit will be the number of 2’s...all the way to the
ninth digit. The tenth digit will be the number of 0’s in the number.
![]()
Problem
27:

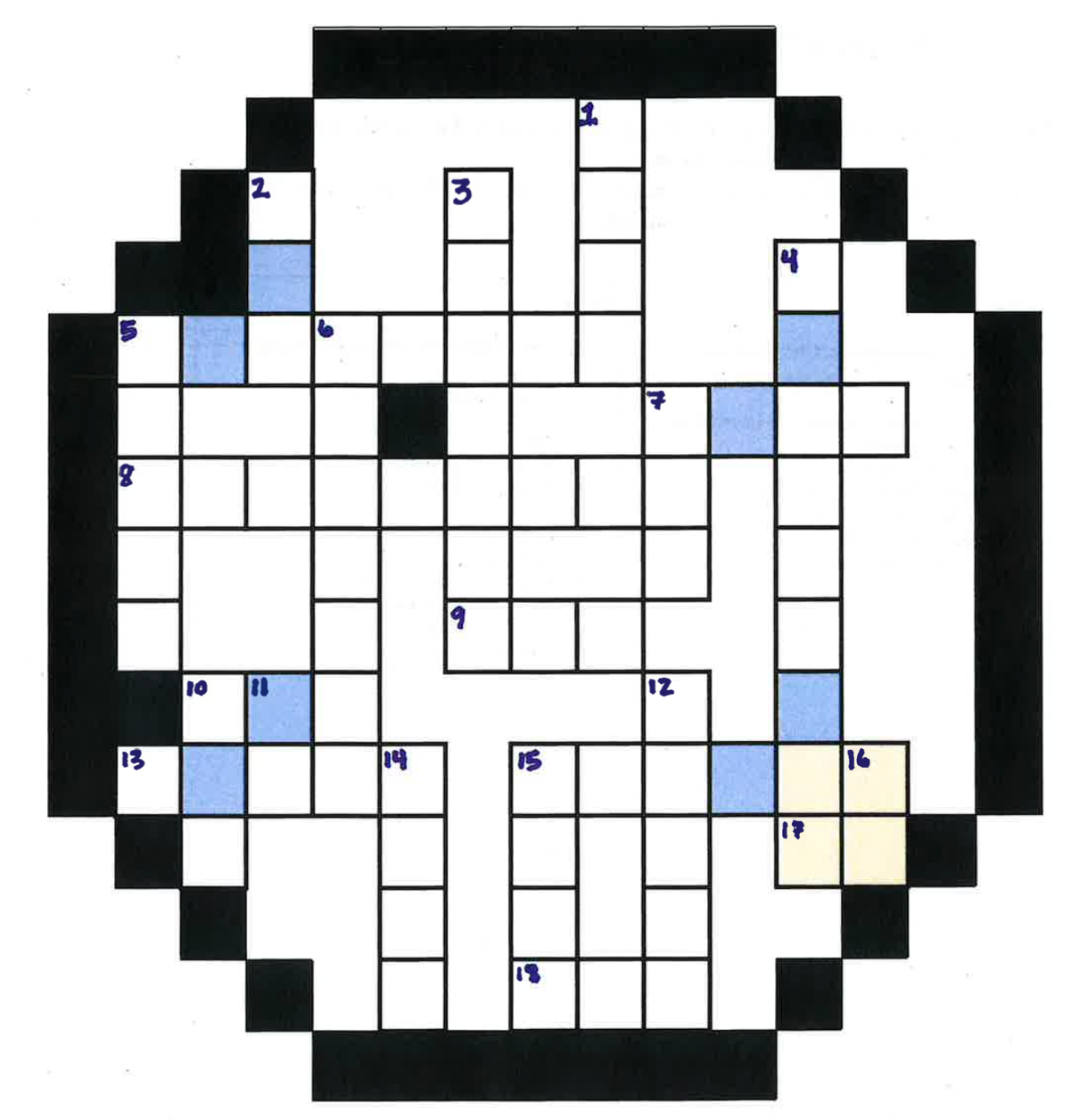
Problem
26:
The problem below is another winner of the POTW student
video solution contest.
Pablo has three different colored marbles with a
ratio of 2 red marbles to 5 green marbles to 7 orange marbles. He has 308
marbles all together.
Pablo decides to give his friend one tenth of one of his colors, one fourth of
one of his colors, and one seventh of one of his colors.
If Pablo only gives his friend marbles in integer amounts, what is the new
ratio of Pablo's marbles in lowest terms? (Please list your answer in the
order: red, green, orange).
Problem
25:
This week’s POTW was a past SAT question. Hint: The answer is not listed below!

Problem
24:
The problem below is another winner of the POTW student
video solution contest.
Ms. Gradek asks her
percussionists to do a practice routine called, "8 on a Hand." For
this drill, drummers need to hit the drum with the drumstick 8 times with one
hand and then do the same on the other hand. They will do this twice for each
hand. Percussionists then need to repeat this exercise with "7 on a
Hand", then "6 on a Hand", and so on, until they've done "1
on a hand."
Since students practice EVERY DAY, on which day 😉
will a drumstick hit the pad for 2024th
time?
Problem
23:
The problem below is another winner of the POTW student
video solution contest.
Three 3-digit numbers sum to 900.
You may only use the digits 1-9 once. What is the largest 3-digit number
possible? 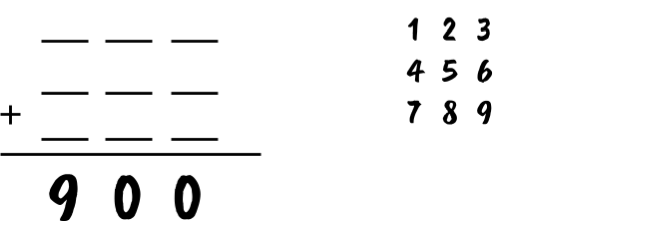 Click here for
video solution
Click here for
video solution
Problem 22:
The problem below is
another winner of the POTW student video solution contest.
Uma and Ellery are both softball players. Uma goes to
the batting cages every three days and Ellery goes to the batting cages every
five days.
How many times do they meet up in 6 months if they go on January 1st together?
**Remember 2024 is a leap year, February has 29 days.**
Problem
21:
Mr. Harris was creating a soup-or-salad bowl out of
clay for a class of forty 9-year-olds. Chiefly, he wanted the bowl to have a
uniform thickness. On Sunday he ushered in the half sphere to his class: the
bowl was a hemisphere with a diameter of 6 cm and a thickness of 1 cm.
How many cubic centimeters of clay did Mr. Harris use?
Hint: Mr. Hurley used his knowledge of the volume of
a sphere and the strategy to draw a picture to solve this POTW.
![]()
Problem
20:
(This
is a problem from the 2024 Latin MS Math Contest.)
Mr. Arthur Mack noticed that next year he
will be 𝑍 years old in the year
𝑍2.
In what year was Mr. Arthur Mack born?
Problem
19:
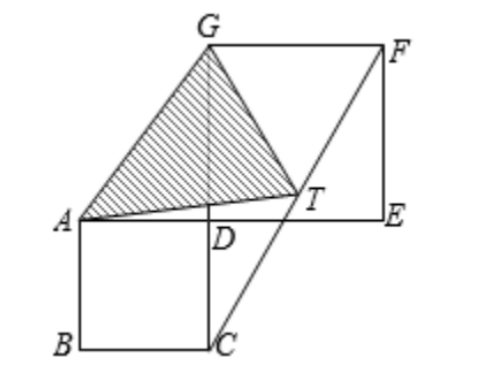
(This is a problem from the 2024 Latin MS Math Contest.)
Given two squares ABCD and DEFG with sides 6 cm and 8
cm, respectively.
Let T be the midpoint of line Segment CF.
Find the area of triangle ATG.
Problem
18:
The MS faculty split up into two groups and are playing a game of Toofball. By throwing the toof, teams can score 7 points and by kicking the toof, teams can score 3 points. Both teams currently have double digit totals.
What is the only score that the score cannot be right now?
Problem
17:
The problem below is another winner of the POTW student
video solution contest.
A cryptarithm is a mathematical puzzle in which the digits of an arithmetic problem have been replaced by letters.
In the puzzle below, each letter stands for a
different digit. (Note: 0 cannot be a leading digit)
Find ABCD.
𝐴,𝐵𝐶𝐷 × 7 = 𝐵𝐷,𝐵𝐷𝐷
Problem
16:
Julian and his father were born 36 years apart
between 1900 and 2000. The last two digits of their birth years are in reverse
order. How many possible birth years could Julian have been born in?
Problem
15:
On New Year’s Eve the date read 12/31/23...but not everywhere!
Many international countries wrote the date: 31/12/23
DD/MM/YY (Day, Month, Year).
What is the next date in this style (DD/MM/YY) in
which the date reads ABCABC?
(Note: A, B, C are all distinct and not equal to 0.)
Problem
14:
This is the last in a series of three POTW’s about puzzles. (This problem is literally about puzzles.)
A puzzle piece can have three different possibilities
on each side:

The puzzle piece below has one flat edge, two outies,
and one innie. (Note: It does not become a different
piece by rotating.)

How many different puzzle pieces are possible? (Hint:
A puzzle piece at most can only have two flat edges.)
Click here for video solution.
Problem
13:
This is the second in a series of three POTW’s about puzzles.
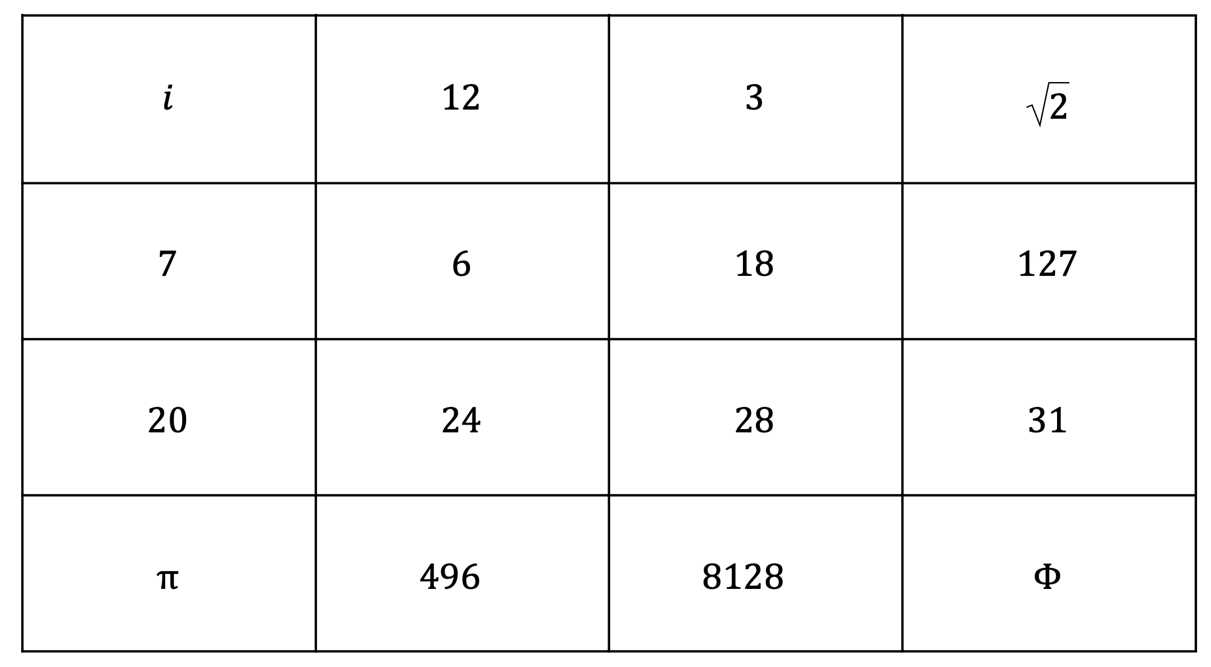
Problem: Number Theory Connections
The NYTimes has developed a new puzzle this year in
which sixteen items are organized into four groups of four. Each group shares a
certain ‘connection.’ Find the four ‘connections’ in the number version below.
Problem
12:
This is the first in a series of three POTW’s about puzzles.
Problem: Perfect Pangrams
The sentence: “The
quick brown fox jumps over the lazy dog” is
a pangram because it uses all 26 letters in the English alphabet. However, it
is not a perfect pangram.
A perfect pangram uses each letter exactly once.
The NYTimes Spelling Bee is a puzzle in which you try to create words from
seven letters in which you must use the middle letter. How many different ways
can you create a perfect pangram from the seven letters in the NYTimes Spelling
Bee puzzle?

Problem
11:
Problem: The “Mean” Taft Bus
The 5th graders are headed to Lorado
Taft this week.
On the bus ride to Taft, the bus driver has an average speed of 40 mph.
However, on the way home the bus driver is speedy, so the average speed is 60
mph.
What was the average speed of the bus for the entire trip?
(Hint: The solution is NOT 50 mph)
Problem 10:
The problem below is another winner of the POTW student
video solution contest.
Problem: "The Prime Number Pyramid"
Imagine constructing a pyramid of prime numbers with
rows as follows:
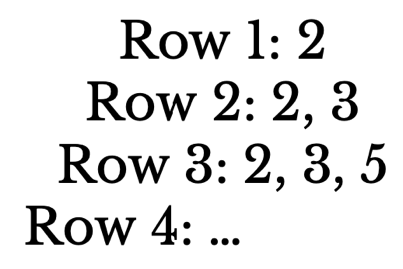
In each row, the prime numbers should be placed in ascending order. The pyramid continues until you reach a row where the sum of the prime numbers in that row exceeds 100.
Find the highest row of the pyramid in which the sum
of the prime numbers in that row does not exceed 100.
Problem
9:
Mr. Hurley set out a bowl of candy in the teacher’s lounge with a sign that said,
“If there are an odd amount
of candies, take one!
If there are an even amount of candies, take half of what is left.”
Eight lucky faculty members were able to have candy
before the bowl was empty.
How many different possible starting amounts of candy could Mr. Hurley have put
in the bowl?
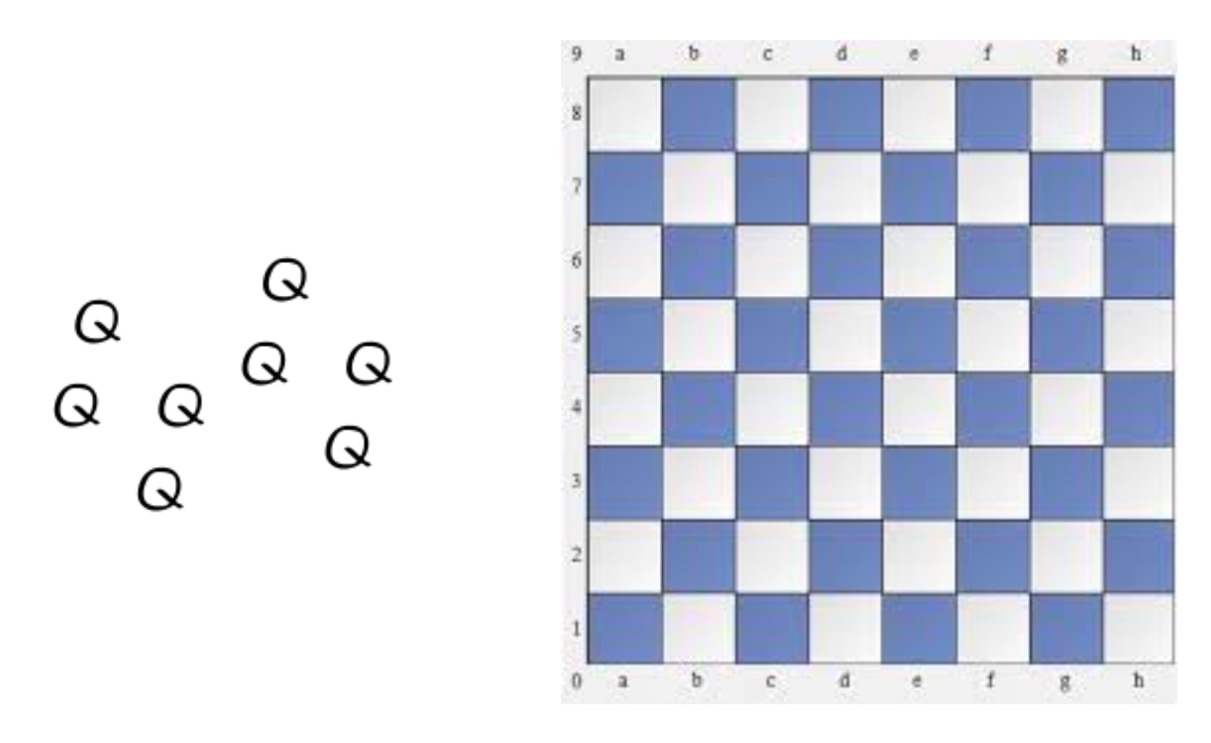
Problem
8:
Chess club is starting this week!
(Days 1 & 5 during your lunch block in the math lab.)
Here is a famous chess problem with a twist... There
are 92 unique solutions of placing 8 queens on a chessboard so that none of the
queens are in the same row, column, or diagonal.
However, there is only one symmetrical solution! (rotational and reflectional
symmetry)
Show the symmetrical solution.
Problem
7:
The problem below is another winner of the POTW student
video solution contest.
What time in the day is the hour equal to the sum of the minutes digits, and the minutes digits divided by two is equal to the hour?
Examples:
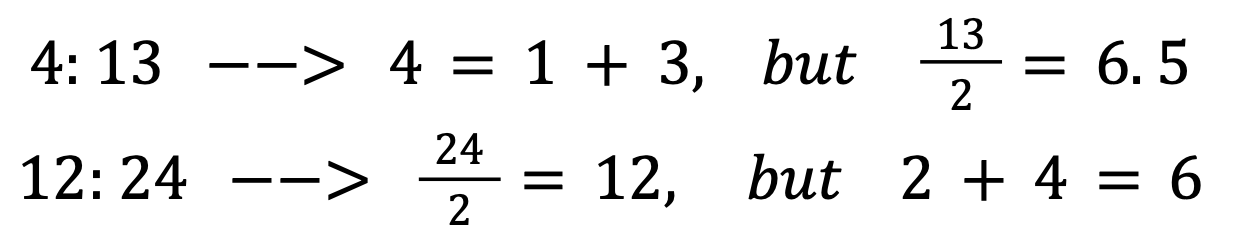
Problem
6:
A lucky date is one in which the month multiplied by
the day is equal to the last two digits of the year.
In 2023, the only lucky date is January 23rd, 2023. (What an unlucky year...I
wonder why that is...)
How many lucky days will there be in 2024?
Bonus: What’s the luckiest possible year?
Problem
5:
Happy October!
Use the 8 pieces so only October 1st remains visible.
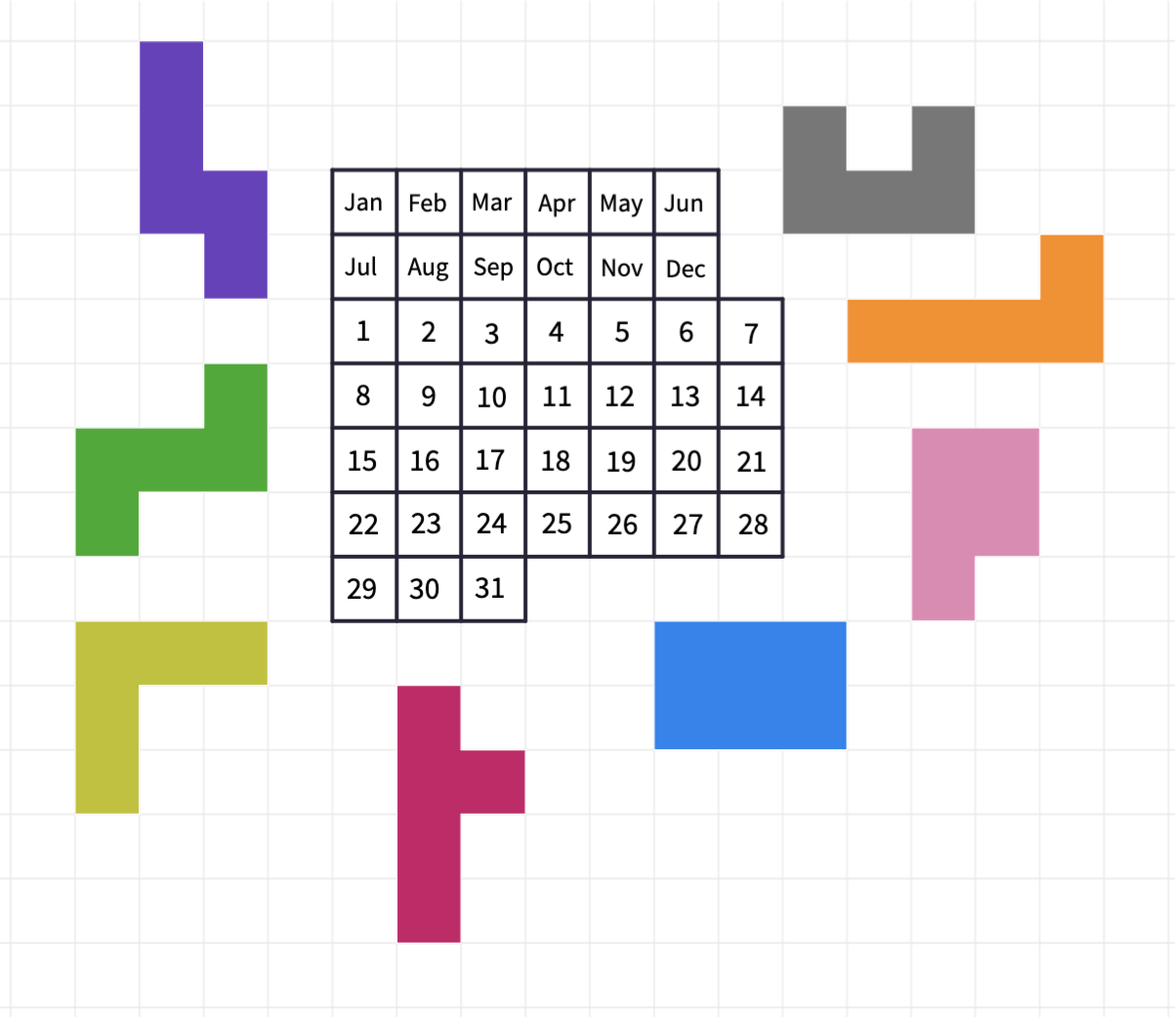
(An interactive version of this problem is found here: https://mathigon.org/polypad/A62G5zIdDPthg)
Problem 4:
Euler's number, when taken to one decimal place and then multiplied by 10, becomes a two-digit number that is the first composite number not divisible by any of its digits and is the only positive integer that is three times the sum of its digits.
What is that two-digit number?

Bonus: Why is this logo here?
Problem 3:
How many palindromic prime numbers have an even amount of digits?
(Hint #1: RACECAR & 99 are both palindromes.)
(Hint #2: Prime numbers have exactly two factors.)
(Hint #3: 88 & 675,309 both have an even amount of
digits)
Problem 2:
Herman was chewing on some bubble gum. Along came a
number of his friends, Sherman, Thurman, Vernon, and Frank.
It took Herman 2 minutes to cut a new strip of gum into 5 pieces so that
everyone had a piece. How long would it take Herman to cut the entire roll of
bubble gum into 100 pieces?
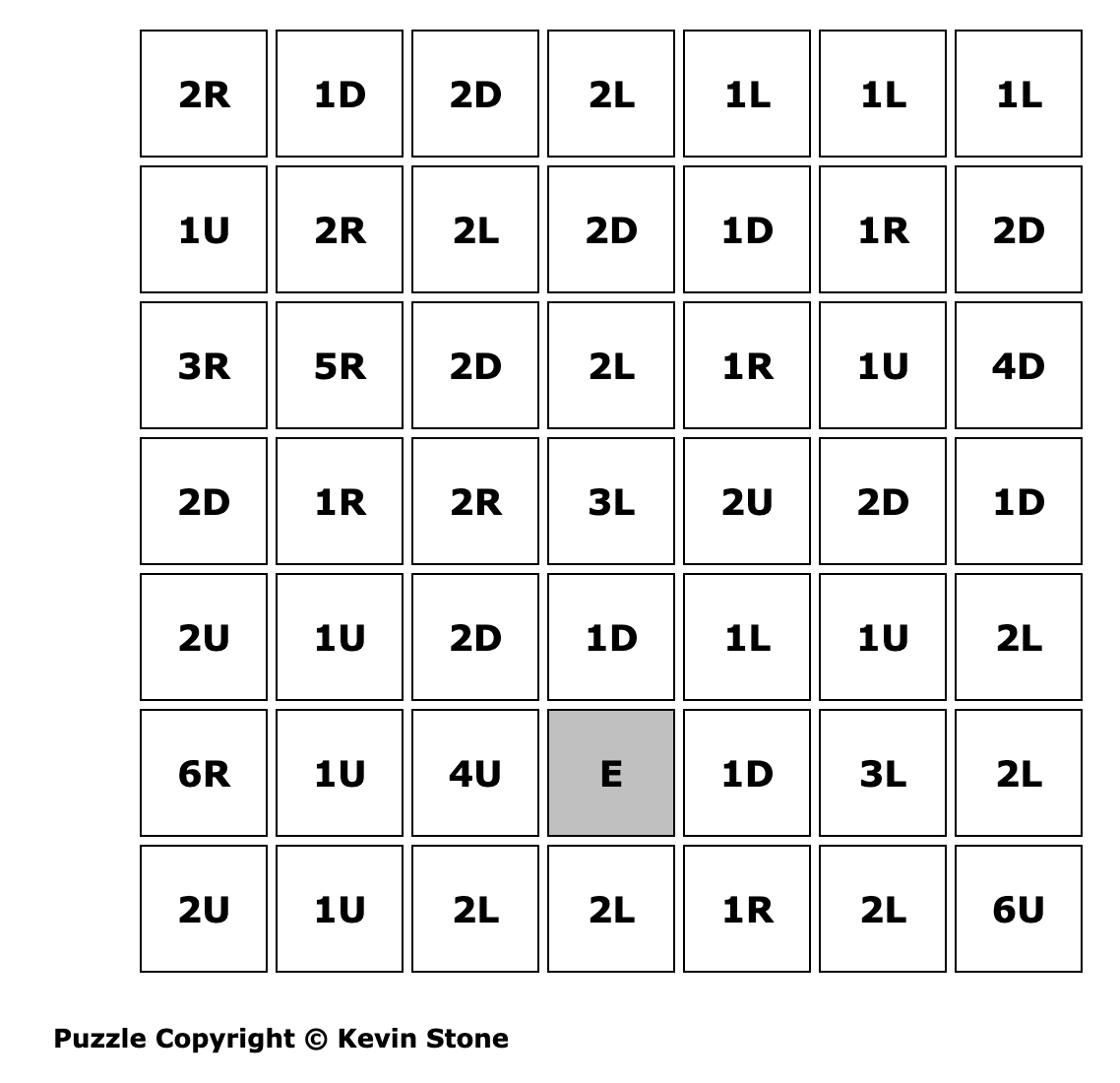
Problem 1:
This
week’s problem is courtesy of Kevin Stone from Brainbashers.
Which button
must you start with in order to press all buttons once and end on the "E'?
(Hint: 2R =
move two to the right)